Algorithmen
Ein Algorithmus ist ein schrittweises Verfahren zum Lösen eines Problems durch ein spezielles Regelwerk. Im Alltag begegnen wir Algorithmen in Form von Gebrauchsanweisungen oder Rezepten. Die Verfahren sind heute wie die Computer-Hardware eine Technologie, die in den unterschiedlichsten Gebieten eingesetzt werden. Eine einfache Aufgabe ist beispielsweise das alphabetische Sortieren einer Menge von Wörtern. Algorithmen können komplexe Aufgaben bearbeiten, wie das Steuern eines autonomen Roboters, die Analyse von Gensequenzen in der Bioinformatik oder das Untersuchen von kosmischen Strahlungen in der Physik.Heute stehen Algorithmen im Zentrum vieler modernen digitaler Produkte. Die Begriffe Digitalisierung, Industrie 4.0, Künstliche Intelligenz oder Big Data haben eins gemeinsam: Sie beschreiben das Auswerten von großen Datenmengen durch intelligente Algorithmen. Beispiele sind selbstfahrende Autos, autonome Robotersysteme, medizinische Diagnosesysteme oder das Internet der Dinge. Im Zeitalter der Digitalisierung entscheidet die Qualität der Algorithmen darüber, wie gut ein technisches Produkt oder eine digitale Dienstleistung funktioniert.
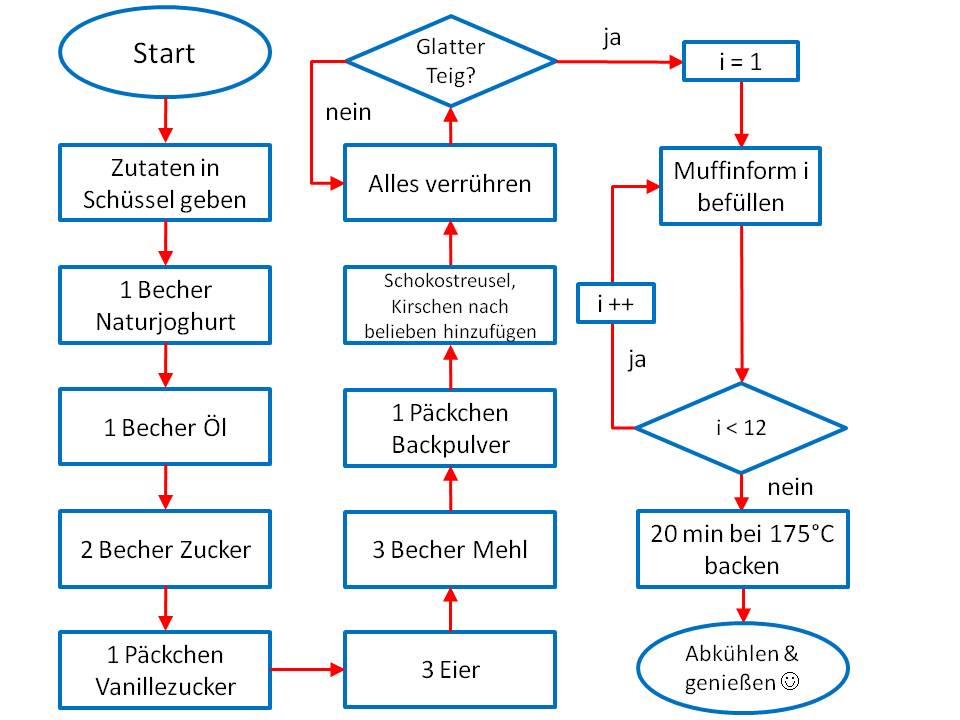
Prinzip eines Algorithmus zum Backen von Muffins (Rezept und Bild von Sonja Jenisch)
Auf einen Blick
Algorithmen
Algorithmen sind geniale Ideen in Form von speziellen Handlungsanweisungen, um ein konkretes Problem zu lösen.
Computerprogramm
Ein Computerprogramm ist die konkrete Umsetzung des Algorithmus in eine Programmiersprache aus einer Reihe von Anweisungen.
Programmiersprache
Eine Programmiersprache ist eine Sprache, die sich aus syntaktischen Anweisungen nach einem vorgegebenen Muster zusammensetzt.
Quellcode
Der Quellcode mit den konkreten Anweisungen wird mit Hilfe eines Texteditors durch die konkrete Implementierung erstellt.
Compiler
Ein Compiler übersetzt die in dieser Sprache geschriebenen Programme in die Maschinensprache des jeweiligen Rechners.
Wofür Algorithmen eingesetzt werden?
Rechnen
Das Rechnen erfolgt mit einer Schritt für Schritt Anleitung zum Auswerten einer mathematischen Formel oder eines speziellen Rechenverfahrens. Beispiele sind das Ermitteln von statistischen Werten, geometrischen Größen oder technischen Kennzahlen in den unterschiedlichsten Anwendungen.
Suchen
In Optimierungsproblemen sind Suchverfahren zum Bestimmen einer möglichst optimalen Lösung bedeutend.
Suchprobleme sind das Ermitteln einer günstigen Route zwischen zwei Ortspunkten oder das Berechnen der optimalen Reihenfolge der Arbeitsschritte in der Produktionsplanung.
Planen
Unter dem Planen versteht man die systematische Vorgehensweise zur Analyse und Lösung von konkreten Problemstellungen. Beispiele sind das Erstellen von optimalen Produktionsplänen in der industriellen Produktion oder das Entwickeln einer effizienten Lagerhaltung.
Verschlüsseln
Beim Verschlüsseln wird mit einem geheimen Schlüssel der sogenannte Klartext in einen Geheimtext umgewandelt.
Verfahren zum Verschlüsseln sind für das sichere Übertragen von Daten im Internet und in anderen Kommunikationsnetzen sehr wichtig.
Komprimieren
Die Verfahren zur Datenkompression reduzieren eine Menge von digitalen Daten im Bezug auf Speicherplatz.
Für das effiziente Speichern und ein schnelles Übertragen von Text-, Bild- oder Videodaten sind Kompressionsalgorithmen von unschätzbarem Wert.
Simulieren
Die Simulation ist eine Methode zur rechnergestützten Analyse von komplexen Systemen, die für die analytische Berechnungen zu aufwendig sind.
Das Optimieren von Baugruppen bzw. Fertigungszeiten oder das Anwenden von FEM bzw. CFD-Simulationen sind Anwendungsgebiete.
Klassifizieren
Unter der Klassifikation verstehen wir das Einordnen von Datensätzen in eine Kategorie oder Gruppe. Beispiele sind das Beurteilen des Gesundheitszustands von Patienten anhand von Untersuchungsergebnissen oder das Erkennen von Mustern auf Bildern oder Schriftzeichen.
Lernen
Das maschinelle Lernen entwickelt Computerprogramme, die aus Trainingsbeispielen lernen und anschließend die gelernten Dinge auf neue Probleme anwenden.
Das Erkennen von Objekten auf Bildern oder das Steuern eines Roboters sind zentrale Lernaufgaben.
Vorhersagen
In Vorhersageproblemen extrahieren Algorithmen aus Datenmengen bestimmte Informationen, um zukünftige Trends abzuschätzen.
Zentrale Beispiele sind die Vorhersage und Planen von Wartungseinsätzen oder die schnellere Ursachenforschung für Fehlerquellen.
Empfehlen
Empfehlungssysteme werden in Online-Shops oder sozialen Netzwerken sehr erfolgreich eingesetzt. Das Ziel von Empfehlungssystemen ist das Steigern der Rückmeldungsquote bei Marketingmaßnahmen und das Verringern der Kosten einer Marketingmaßnahme.
Kommunizieren
Selbstlernende kognitive Systeme kommunizieren mit Menschen und anderen Computern, erinnern sich an frühere Interaktionen und ziehen eigenständig Schlüsse. Beispiele sind Systeme zur medizinischen Diagnostik oder Rat- und Auskunftsgeber in Servicezentren.
Schließen
Unter dem Schließen verstehen wir einen Verarbeitungsmechanismus zum Ableiten von neuem Wissen aus einer Wissensbasis. Diese Form der Informationsverarbeitung besitzt viele Anwendungen im Bereich der Künstlichen Intelligenz und der Mensch-Maschine-Kommunikation.
Entwurfsmuster für Algorithmen
Der Entwurf von effizienten Algorithmen setzt viel Erfahrung und Wissen über algorithmische Methodiken voraus. Viele algorithmische Verfahren sind nach dem Baukastenprinzip aufgebaut. Hierbei wenden wir spezielle Grundalgorithmen wie Sortieren, Suchen oder Verfahren der Linearen Algebra als Unterroutinen an.. Mit Algorithmenmustern entwickeln wir für bestimmte Problemklassen einen abstrakten Programmrahmen, der für konkrete Probleme auszufüllen ist.Iterative Algorithmen

Iterative Algorithmen durchlaufen Abschnitte innerhalb einer einzigen Ausführung mehrfach.
Diese Art der Algorithmen verwenden Schleifen zur Wederholung von Anweisungen oder Anweisungsfolgen.
Beispiele: Lösen von linearen Gleichungssystemen, Sortieren von Objekten (z.B. BubbleSort), numerische Berechnung von Integralen.
Beispiele: Lösen von linearen Gleichungssystemen, Sortieren von Objekten (z.B. BubbleSort), numerische Berechnung von Integralen.
Rekursive Algorithmen
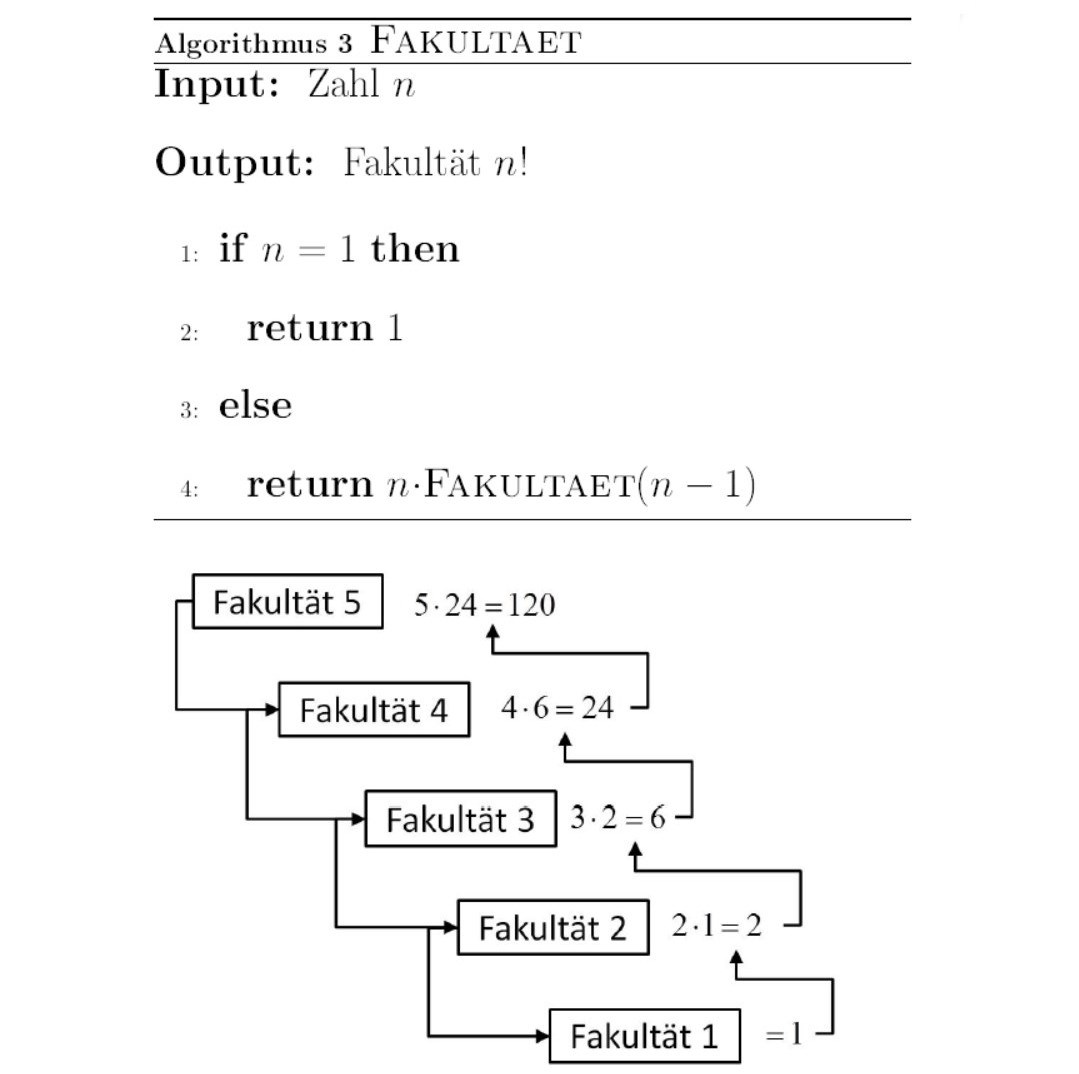
Ein rekursiver Algorithmus enthält Abschnitte, die sich selbst direkt oder indirekt aufrufen. Das Prinzip der Rekursion ist ein zentrales Konzept der Mathematik, um
Formeln kurz und elegante zu formulieren.
Beispiele: Berechnen der Fakultätsfunktion, Prüfen einer Zeichenkette auf ein Palindrom, Umwandeln von Zahlen in eine andere Basis.
Beispiele: Berechnen der Fakultätsfunktion, Prüfen einer Zeichenkette auf ein Palindrom, Umwandeln von Zahlen in eine andere Basis.
Greedy Algorithmen

Ein Greedy-Algorithmus (dt. gierig) wählt aus mehreren Alternativen diejenige aus, die im Moment am besten erscheint. Die Heuristik bestimmt damit eine lokal optimale Entscheidung in der Hoffnung, dass diese zu einer optimalen globalen Lösung führt.
Beispiele: Geldrückgabe an Supermarktkassen, Planen von Aufträgen mit Endterminen, Bestimmen einer optimalen Menge von Transportgegenständen.
Beispiele: Geldrückgabe an Supermarktkassen, Planen von Aufträgen mit Endterminen, Bestimmen einer optimalen Menge von Transportgegenständen.
Dynamisches Programmieren
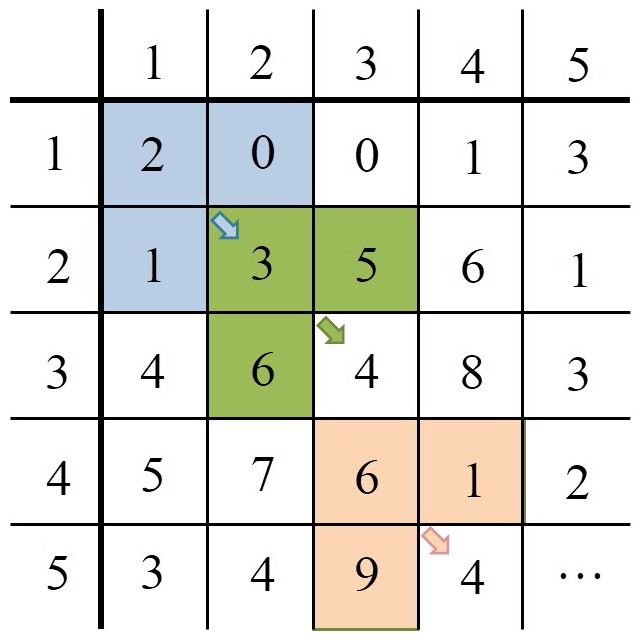
Das dynamische Programmieren bestimmt die optimalen Lösungen der kleinsten Teilprobleme direkt.
Diese Teilergebnisse speichert das Verfahren in einer Tabelle.
Anschließend setzt sich die Lösung des nächstgrößeren Teilproblems aus diesen Ergebnissen zusammen.
Beispiele: Bestimmen einer optimalen Rundreise, Ermitteln einer optimalen Menge von Transportgegenständen.
Beispiele: Bestimmen einer optimalen Rundreise, Ermitteln einer optimalen Menge von Transportgegenständen.
Teile und Herrsche
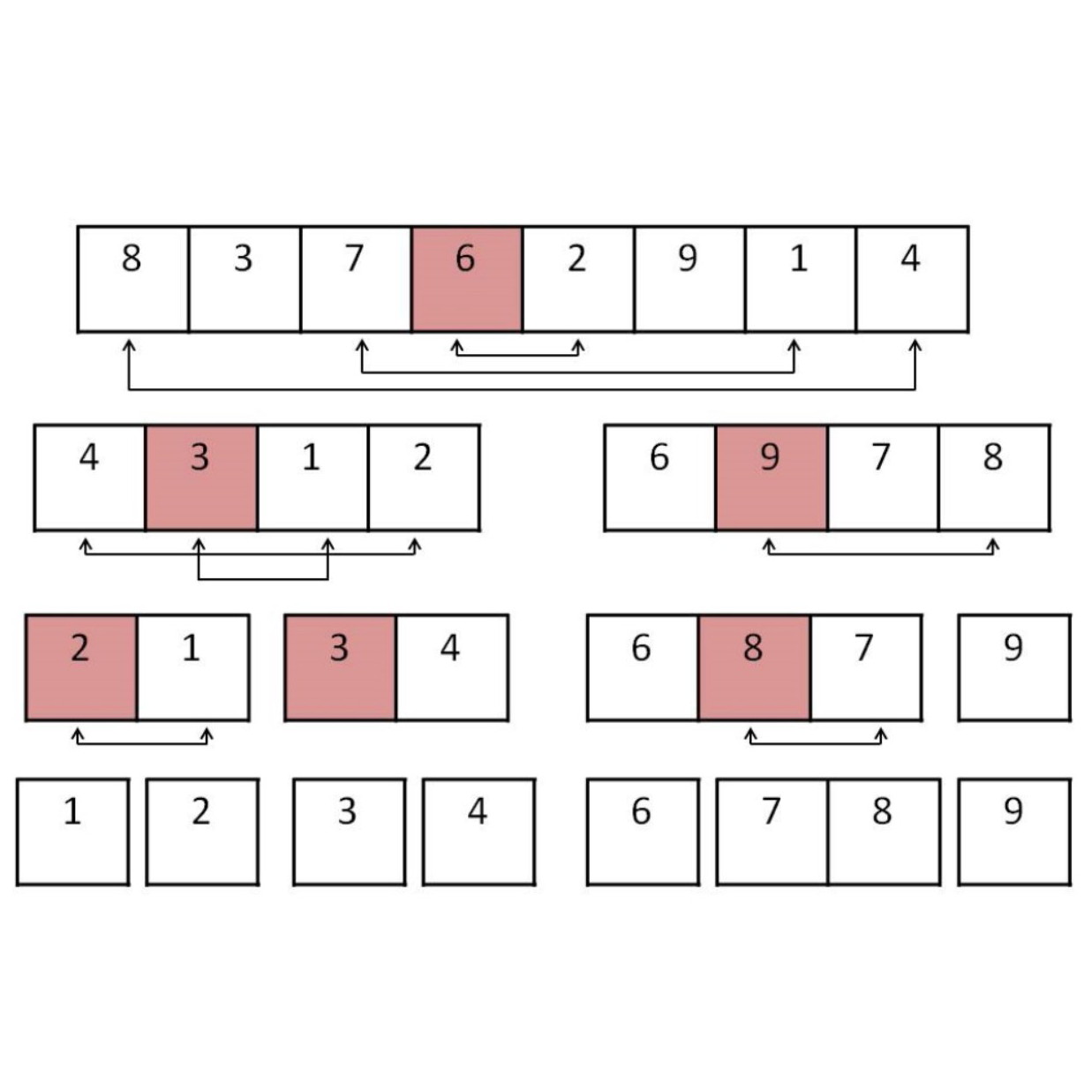
Ein Problem wird so lange rekursiv in kleinere und einfachere Teilprobleme aufgeteilt ("teile"), bis diese einfach zu lösen sind ("herrsche"). Aus den resultierenden Teillösungen wird eine Lösung für das Gesamtproblem konstruiert.
Beispiele: Sortieren von Objekten mit QuickSort, Multiplikation von Zahlen und Matrizen, schnelle Fouriertransformation (FFT) in der Signal- und Bildverarbeitung.
Beispiele: Sortieren von Objekten mit QuickSort, Multiplikation von Zahlen und Matrizen, schnelle Fouriertransformation (FFT) in der Signal- und Bildverarbeitung.
Backtracking
Das Backtracking ist eine systematische Suchtechnik, die einen Lösungsraum vollständig absucht. Falls absehbar ist, dass eine Teillösung nicht zu einer Gesamtlösung führt, werden die letzten Schritte zurückgenommen und stattdessen ein alternativer Weg probiert.
Beispiele: Untersuchen von Strategiespielen, Bestimmen einer optimalen Menge von Transportgegenständen, Färben einer Landkarte.
Beispiele: Untersuchen von Strategiespielen, Bestimmen einer optimalen Menge von Transportgegenständen, Färben einer Landkarte.